8086 汇编-进制和数据宽度

本帖最后由 啥都不会 于 2022-4-21 20:57 编辑

本帖最后由 啥都不会 于 2022-4-17 23:51 编辑

本帖最后由 啥都不会 于 2022-4-17 23:47 编辑

前言：

本人菜鸟一个，在这里发一些汇编的学习笔记。笔记中会尽量记录学习的知识点，如有问题欢迎大家指出，一起讨论学习。 8086汇编笔记参照的是 "杨季文《80X86汇编语言程序设计教程》" 和滴水的16位汇编基础培训课程。

以下为主题内容：

进制

数的本质是一个用来统计事物的规模、筹划事物的大小，以及认识事物的变化规律的符号系统。进制和各种运算方法都是由数字演化而来，主要是为了快速解决现实中的实际问题。

进制的定义

十进制：由十个符号组成，分别是 0、1、2、3、4、5、6、7、8、9 逢十进一

十六进制：由十六个符号组成，分别是 0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F 逢十六进一

N 进制的定义：由 N 个符号组成，分别是 0~N 逢 N 进一

进制是由人定义的，进制的字符、顺序都可自定义。

二进制从 0 往后写 30 个数

0	1
10	11
100	101	110	111
1000	1001	1010	1011	1100	1101	1110	1111
10000	10001	10010	10011	10100	10101	10110	10111	11000	11001	11010	11011	11100	11101	11110

八进制从 0 往后写 80 个数

0	1	2	3	4	5	6	7
10	11	12	13	14	12	16	17
20	21	22	23	24	25	26	27
30	31	32	33	34	35	36	37
40	41	42	43	44	15	46	47
50	51	52	53	54	52	56	57
60	61	62	63	64	65	66	67
70	71	72	73	74	75	76	77
100	1001	1002	1003	1004	1005	1006	1007
200	2001	2002	2003	2004	2005	2006	2007

自定义进制

3 进制

定义：由 3 个符号组成，分别是：2、0、1，逢 3 进 1

顺序	0	1	2
符号	2	0	1
	02	00	01
	12	10	11
	022	020	021
	002	000	001
	012	010	011
	122	120	121
	102	100	101
	112	110	111
	0222	0220	0221
	0202	0200	0201
	0212	0210	0211
	0022	0020	0021
	0002	0000	0001
	0012	0010	0011
	0122	0120	0121
	0102	0100	0101
	0112	0110	0111
	1222	1220	1221
	1202	1200	1201
	1212	1210	1211
	1022	1020	1021
	1002	1000	1001
	1012	1010	1011
	1122	1120	1121
	1102	1100	1101
	1112	1110	1111

以行为准，个位数进 1；以第一列为准最高位进 1（进1表示：该值的后一位数）

4 进制

定义：由 4 个符号组成，分别是：3、8、2、4，逢 4 进 1

顺序	0	1	2	3
符号	3	8	2	4
	83	88	82	84
	23	28	22	24
	43	48	42	44
	833	838	832	834
	883	888	882	884
	823	828	822	824
	843	848	842	844
	233	238	232	234
	283	288	282	284
	223	228	222	224
	243	248	242	244
	433	438	432	434
	483	488	482	484
	423	428	422	424
	443	448	442	444
	8333	8338	8332	8334
	8383	8388	8382	8384
	8323	8328	8322	8324
	8343	8348	8342	8344
	8833	8838	8832	8834

进制运算

进制运算本质就是定义一个运算表，然后根据表格去查结果，我们只要知道进制的加法表和乘法表就可以做运算。

八进制运算

加法表

1+1=2
1+2=3	2+2=4
1+3=4	2+3=5	3+3=6
1+4=5	2+4=6	3+4=7	4+4=10
1+5=6	2+5=7	3+5=10	4+5=11	5+5=12
1+6=7	2+6=10	3+6=11	4+6=12	5+6=13	6+6=14
1+7=10	2+7=11	3+7=12	4+7=13	5+7=14	6+7=15	7+7=16

乘法表

1*1=1
1*2=2	2*2=4
1*3=3	2*3=6	3*3=11
1*4=4	2*4=10	3*4=14	4*4=20
1*5=5	2*5=12	3*5=17	4*5=24	5*5=31
1*6=6	2*6=14	3*6=22	4*6=30	5*6=36	6*6=44
1*7=7	2*7=16	3*7=25	4*7=34	5*7=43	6*7=52	7*7=61

加法运算（查找八进制加法表）

277

+   333

--------

    632


运算步骤：

7+3=12（写2进1）

7+3=12+1=13（写3进1）

2+3+1=6

乘法运算（查找八进制加法表）

276

*    54

---------

   1370

  1666

---------

  20250


运算步骤：

4*6=30（写0进3）

4*7=34+3=30+(4+3)=30+7=37（写7进3）

2*4=10+5=10+(0+3)=13


5*6=36（写6进3）

5*7=43+3=40+(3=3)=46（写6进4）

5*2=12+4=10+(2+4)=16

减法运算（查看八进制加法表）

236

-    54

---------

    162


运算步骤：

4+n=6；n=2

5+n=13；n=6

除法运算（查看八进制乘法表）

234

/     4

---------

     47


运算步骤：

4*n=23；4*4=20（余3）

4*n=34；4*7=34

进制运算一定要按照上面的方法，查表中的值，如果口算不小心就会把 2+8 算成 10

七进制运算

加法表

1+1=2
1+2=3	2+2=4
1+3=4	2+3=5	3+3=6
1+4=5	2+4=6	3+4=10	4+4=11
1+5=6	2+5=10	3+5=11	4+5=12	5+5=13
1+6=10	2+6=11	3+6=12	4+6=13	5+6=14	6+6=15

乘法表

1*1=1
1*2=2	2*2=4
1*3=3	2*3=6	3*3=12
1*4=4	2*4=11	3*4=15	4*4=22
1*5=5	2*5=13	3*5=21	4*5=26	5*5=34
1*6=6	2*6=15	3*6=24	4*6=33	5*6=42	6*6=51

七进制练习题

23456+54356


    23456

+   54356

----------

   111145



  5621

+  654

---------  

  4634


    234

*    65

---------

   1536

  2103

---------

  22566

十六进制运算

加法表

1+1=1
1+2=3	2+2=4
1+3=4	2+3=5	3+3=6
1+4=5	2+4=6	3+4=7	4+4=8
1+5=6	2+5=7	3+5=8	4+5=9	5+5=A
1+6=7	2+6=8	3+6=9	4+6=A	5+6=B	6+6=C
1+7=8	2+7=9	3+7=A	4+7=B	5+7=C	6+7=D	7+7=E
1+8=9	2+8=A	3+8=B	4+8=C	5+8=D	6+8=E	7+8=F	8+8=10
1+9=A	2+9=B	3+9=C	4+9=D	5+9=E	6+9=F	7+9=10	8+9=11	9+9=12
1+A=B	2+A=C	3+A=D	4+A=E	5+A=F	6+A=10	7+A=11	8+A=12	9+A=13	A+A=14
1+B=C	2+B=D	3+B=E	4+B=F	5+B=10	6+B=11	7+B=12	8+B=13	9+B=14	A+B=15	B+B=16
1+C=D	2+C=E	3+C=F	4+C=10	5+C=11	6+C=12	7+C=13	8+C=14	9+C=15	A+C=16	B+C=17	C+C=18
1+D=E	2+D=F	3+D=10	4+D=11	5+D=12	6+D=13	7+D=14	8+D=15	9+D=16	A+D=17	B+D=18	C+D=19	D+D=1A
1+E=F	2+E=10	3+E=11	4+E=12	5+E=13	6+E=14	7+E=15	8+E=16	9+E=17	A+E=18	B+E=19	C+E=1A	D+E=1B	E+E=1C
1+F=10	2+F=11	3+F=12	4+F=13	5+F=14	6+F=15	7+F=16	8+F=17	9+F=18	A+F=19	B+F=1A	C+F=1B	D+F=1C	E+F=1D	F+F=1E

乘法表

1*1=1
1*2=2	2*2=4
1*3=3	2*3=6	3*3=9
1*4=4	2*4=8	3*4=C	4*4=10
1*5=5	2*5=A	3*5=F	4*5=14	5*5=19
1*6=6	2*6=C	3*6=12	4*6=18	5*6=1E	6*6=24
1*7=7	2*7=E	3*7=15	4*7=1C	5*7=23	6*7=2A	7*7=31
1*8=8	2*8=10	3*8=18	4*8=20	5*8=28	6*8=30	7*8=38	8*8=40
1*9=9	2*9=12	3*9=1B	4*9=24	5*9=2D	6*9=36	7*9=3F	8*9=48	9*9=51
1*A=A	2*A=14	3*A=1E	4*A=28	5*A=32	6*A=3C	7*A=46	8*A=50	9*A=5A	A*A=64
1*B=B	2*B=16	3*B=21	4*B=2C	5*B=37	6*B=42	7*B=4D	8*B=58	9*B=63	A*B=6E	B*B=79
1*C=C	2*C=18	3*C=24	4*C=30	5*C=3C	6*C=48	7*C=54	8*C=60	9*C=6C	A*C=78	B*C=84	C*C=90
1*D=D	2*D=1A	3*D=27	4*D=34	5*D=41	6*D=4E	7*D=5B	8*D=68	9*D=75	A*D=82	B*D=8F	C*D=9C	D*D=A9
1*E=E	2*E=1C	3*E=2A	4*E=38	5*E=46	6*E=54	7*E=62	8*E=70	9*E=7E	A*E=8C	B*E=9A	C*E=A8	D*E=B6	E*E=C4
1*F=F	2*F=1E	3*F=2D	4*F=3C	5*F=4B	6*F=5A	7*F=69	8*F=78	9*F=87	A*F=96	B*F=A5	C*F=B4	D*F=C3	E*F=D2	F*F=E1

十六进制练习题

2D4E6

+   CF3A6

-----------

    FC88C



    5FD1

-    E5A

----------

    5177



    2CA

*    A5

---------

    DF2

* 1BE4

---------

  1CC32

自定义10 进制运算

由 10 个符号组成，分别是：！、@、$、%、^、&、*、A、B、C，逢 10 进 1

0	1	2	3	4	5	6	7	8	9
!	@	$	%	^	&	*	A	B	C

加法表

1	2	3	4	5	6	7	8	9
@+@=$
@+$=%	$+$=^
@+%=^	$+%=&	%+%=*
@+^=&	$+^=*	%+^=A	^+^=B
@+&=*	$+&=A	%+&=B	^+&=C	&+&=@!
@+*=A	$+*=B	%+*=C	^+*=@!	&+*=@@	+\=@$
@+A=B	$+A=C	%+A=@!	^+A=@@	&+A=@$	*+A=@%	A+A=@^
@+B=C	$+B=@!	%+B=@@	^+B=@$	&+B=@%	*+B=@^	A+B=@&	B+B=@*
@+C=@!	$+C=@@	%+C=@$	^+C=@%	&+C=@^	*+C=@&	A+C=@*	B+C=@A	C+C=@B

十进制练习题

计算：@$$B + %AC&

@$$B

+   %AC&

---------

    &!$%


B+&=@%：写 % 进 @

$+C=@@+@=@$：写 $ 进 @

$+A=C+@=@!：写 ! 进 @

@+%=^+@=&

总结

说到底进制就是用来描述某个特定的事物。在计算机中程序一开始用的是二进制编写的，之后发现这样写太麻烦而且容易出错。为了解决这个问题，程序员又为计算机写了个十六进表用来简化操作。因此计算机也得到改进，自动将二进制数据转换成十六进制数据，所以现在的二进制文件打开之后都是显示十六进制数据。

二进制和十六进制对应关系

0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

数据宽度

数学上的数字没有大小限制，可以无限大。但是在计算机中，由于受到硬件的制约，数据都是有长度（数据宽度）限制的，超过最大宽度的数据会被丢弃。

有符号数和无符号数

假设计算机只能存储 4 位 2 进制数，分别表示

0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

如下图所示，这个圆是一个 4 位宽度的存储器。

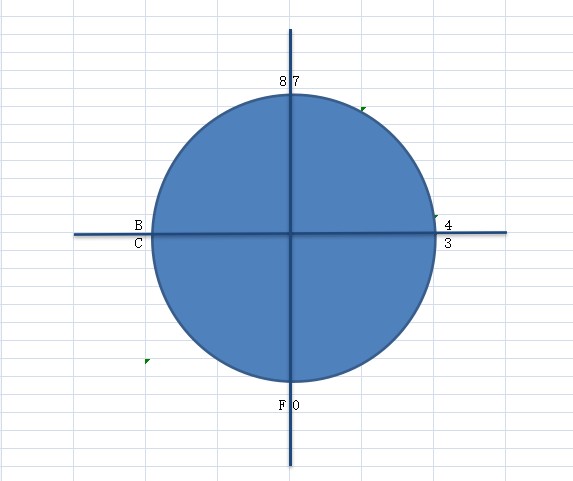
计算机是不会识别正数和负数，它只知道 0 和 1 。正数和负数只是人为的判断这个值是正数还是负数。

无符号数

无符号数就是把存储器的所有空间都用来存正数。例如上面 4 位宽度的存储器，它的无符号数范围就是：0~F

有符号数

有符号数就是把存储器对半分，一半存正数，一半存负数。

就以上面的 4 位存储器为例：你可以理解为把这个 4 位宽度的存储器从中间切成两半，一半存正数、一半存负数。也就是说正数为：0~7，负数为：8~F。

又因为 F 后面的值是 0，所以存储器设计 F 为最大的负数，所以 F = -1。

4 位存储器的存储规律

正数：

0 1 2 3 4 5 6 7

负数：

-1	-2	-3	-4	-5	-6	-7	-8
F	E	D	C	B	A	9	8

F 是最大的负数，因为从存储器上面看 F+1=10000 。4 位存储器存储不了这么大的值，所以会把最高位 1 丢弃，也就是说值最后变成 0 ：

7	6	5	4	3	2	1	0	-1	-2	-3	-4	-5	-6	-7	-8
7	6	5	4	3	2	1	0	F	E	D	C	B	A	9	8
0111	0110	0101	0100	0011	0010	0001	0000	1111	1110	1101	1100	1011	1010	1001	1000

我们从上面的规律中可以看到，当二进制的最高位为 1 的时候值是负数。

8 位存储器的存储规律

8 位宽度表示，假设计算机只能存储 8 位 2 进制数。

1. 它的无符号数是：0~FF
2. 有符号数是：

正数：0~7F（0~127）

负数：FF~80（-1~-128）

字符串的转换

既然计算机存储器存储的数据是有限的，那计算机又是如何将这些十六进制（0和1）输出到屏幕变成我们所认识的字符串呢？

例如：计算机中的一段数据 “0110100001100101011011000110110001101111” 表示什么？

答案是设计一个符号表，把这些不可读的符号和现实中用到的符号关联起来，因此有了 ASCII 编码表。

首先用十六进制，把宽度为 4 位的二进制数据分为一组，转换成 1 个十六进制符号

0110	1000	0110	0101	0110	1100	0110	1100	0110	1111
6	8	6	5	6	C	6	C	6	F

之后再根据 asscii 表，将两个十六进制数据作为一组，转换成我们熟悉的字母 "hello"，以上是计算机做字符串转换的过程。

数据宽度的意义

1. 不在 ASCII 编码表范围内的十六进制

例如我们想要让计算机程序找到内存中的十六进制数 B86A，那我们只能给 16 个二进制数据让计算机去处理判断。

2. 在 ASCII 编码表范围内的十六进制

因为 ASCII 码的出现，将两个十六进制（8 位二进制）宽度的数据分为一组。此时不可读的数据，变成的可读、更容易理解，且有意义的数据。

注：计算机程序只做数据的处理和判断，需要处理多少宽度的数据需要人为判断。

逻辑运算

或（or，|）

概念：只要有一个为 1 ，值就为 1

1001010

or  0101001

-------------

    1101011

与（and，&）

概念：两个都为1时，值为1

1001010

or  0101001

-------------

    0001000

异或（xor，^）

概念：两个不一样时，值为1

1001010

or  0101001

-------------

    1100011

非（not，!）

概念：1变为0,0变为1

not 1001010

-------------

    0110101

左移（<<）

概念，数值向左移一位，低位补 0

值向左移一位


    1001010

<<        1

-------------

    0010100

右移（>>）

概念，数值向右移，高位补 0

值向左移一位


    1001010

>>        1

-------------

    0100101

CPU 运算 2+3 的过程

计算机只认识 0 和 1，那么计算机是如何进行计算的，使得 2(0010)+3(0011)=5(0101)

1. 将两个值进行异或运算，并存储到 R 存储器中

0010

xor 0011

---------

    0001


R：0001

2. 将两个值进行与运算，然后左移 1 位，并存到 X 存储器中

0010

and 0011

---------

    0010


    0010

<<     1

---------

    0100


X：0100

左移之后计算机会判断值是不是 0，如果是 0 就取 R 的值，否则就将值存到 X 存储器中，继续运算

3. 将 R 和 X 中的值进行异或，并存储到 R 存储器中

0001

xor 0100

---------

    0101


R:0101

4. 将两个值进行与运算，然后左移 1 位

0001

and 0100

---------

    0000


    0000

<<     1

---------

    0000

5. 这里左移后值为 0 ，所以结果取 R 的值，结果为 0101=5

步骤分析

xor：相当于将两个值的位进行相加（除了进位）

and：判断有没有进位

<<：左移 1 位，实现进位

判断值是否为0：若值为 0 ，说明这个值不需要进位了，前面的 xor 已经算出结果；若值不为0，说明这个值还需要进位，现在还没有算出结果

逻辑运算的应用

八进制 2-5 在计算机中的结果是多少？为什么？

8 进制，由 8 个字符组成的，逢 8 进 1

0，1，2，3，4，5，6，7

000 001 010 011 100 101 110 111


    010(2)
+   011(-5)
-----------
    101
-----------
    1101(D==-3,符号位扩展为16进制)


因寄存器比较大，所以前面会继续填充符号位直到填满为止，最后结果为：FFFFFFFFFFFFFFFD 转成十进制是 1777777777777777777775

使用异或对 87AD6 进行加密再进行解密，加密秘钥是 5

加密

1000    0111    1010    1101    0110


xor                                 0101

------------------------------------------

    1101    0010    1111    1000    0011

------------------------------------------

    D       2       F       8       3

解密

1101    0010    1111    1000    0011

xor                                 0101

------------------------------------------

    1000    0111    1010    1101    0110

------------------------------------------

    8       7       A       D       6

使用逻辑运算计算 2-3=?（涉及内容，逻辑运算、移位，数据宽度）

减法其实就是加法运算：2-3 = 2+(-3)

1. 值相加

    0010

xor 1101

---------

    1111


2. 计算需要进位的值

    0010

&   1101

---------

    0000


3. 进行进位

    0000
<<     1
--------

    0000


4. 值为 0000 ，不需要继续运算，值最后为 1111=F(-1)

感谢楼主

谢谢分享

感谢楼主

这 makedown 开头的红色标题是不是有问题，发帖的编辑器里面正常的，怎么一发出来就不一样了

谢谢分享

谢谢分享

感谢楼主分享，我瞧瞧

谢谢分享

感谢楼主的热心分享